How to turn a sphere inside-out ? One of the most interesting puzzles in topology.
Updated May 30th, 2016
Please scroll beyond the video and image below for a detailed introduction and explanation.
Over the past seven years, I have enjoyed several enlightening e-mail discussions
about details of my sphere eversion method with Chris Hills (Cambridge, UK.)
Chris recently completed a three-dimensional visualization based on my ideas, which
previously had to rely on my old hand-drawn pixel art to illustrate it. He came up with
a novel way to show how two crossing loops on the sphere's surface are equivalent to
two touching loops, by sliding them into- and out of each other in a brilliant, simple to
understand way. Crossing loops resolving into touching loops is a crucial part of this method
which previously, lacking clear visualization, had been a sticking point for many people.
( see the video at 0:33 and 0:55. )
I suggest you try to follow the steps outlined in this paragraph below, and then watch the video
here, on YouTube - or even in 3D ( which most 3D TVs can display; also, the VLC Media Player
can do Anaglyph 3D - for colored 3d glasses.)
'
TOPOLOGY
The branch of mathematics called topology studies special properties of
shapes and surfaces. In topology the size and to a certain extent the
shape of an object are irrelevant. In particular, two objects or structures
are considered topologically equivalent if one can be stretched and deformed
in a continuous way, to become exactly like the other. Objects like the sphere
and the torus (doughnut) are called two-dimensional manifolds.
Such manifolds, as we imagine them immersed in our familiar 3-dimensional
space, may also appear to pass through themselves, as long as this does not
give rise to intermediate stages with sharp points or creases.
APPROACH
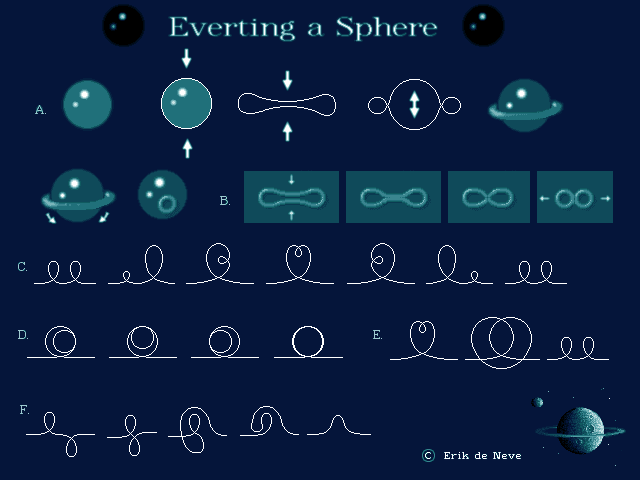
The diagram above shows some steps of my own approach to everting
a sphere (turning it inside-out).
First, try the rough approach of sequence A : push the bottom up, and
the top down, through each other. This results in an everted sphere (in
this case, imagine the inside was painted with a darker color) but also
leaves a ring-shaped fold, which you cannot get rid of just by making
it infinitely small, because that would create a sharp crease. Instead,
we pull the ring down and make it smaller.
Sequence B gives a recipe for doubling such a ring. Squeeze the
ring so its two sides touch and merge (first two pictures).
To see what happens when they merge, look at sequences C, D and E,
which provide cross sections of the two folds, in the same way as the
third and fourth picture in sequence A represent cross sections of the
whole sphere.
When one loop is made smaller, as in C, it is clear how it can traverse
the other, and in that case the two folds will cross each other. But
when pictured differently, the loops can actually lose their identity,
so two folds crossing each other (third picture in B) are topologically
equivalent to parallel folds touching each other (second picture in B).
To make this plausible, imagine how sequence C would change if the
two loops were gradually changed into completely overlapping circles of
the same size, as in the last picture of D.
If this does not convince you, follow C up to the middle picture
and then deform into two separate loops using the alternative in E.
Now, it is impossible to decide whether the loops have switched places
or not.
So, when two merging folds turn into two crossing folds, we can create
the figure 8 shape in the third picture of B. This is easiest to imagine if
we let one loop be much smaller than the other, spiraling around inside
the bigger loop in the manner of diagram C. Now we can tighten the spiral
until the smaller loop dives straight through the bigger loop, at a
90-degree angle. Increasing the angle again in the other direction we can
gradually turn crossing folds into touching folds again, this time vertically,
so we can end up with two rings (last picture). In the youtube video,
this is what happens centered around the 0:46 crossing point.
Once we can envision this, how do we use it to evert a sphere ?
Performing A twice will give the original sphere (outside out) with two
rings, one on the inside and one on the outside. Now, multiply the
outside ring as explained above. Then we can let two opposite rings
eliminate each other. For this, imagine the rings as concentric, one
around the other, then let them come closer and merge as indicated in
F. Now we are left with just one ring on the outside, and all that
remains is to execute sequence A in reverse.
As shown in the video, the procedures above can also be combined in a
much simpler way: perform F backward, to generate two opposite folds from
scratch; stretch one fold out along the surface so that it can touch itself and
"spawn" a ring shaped fold, then have the initial folds eliminate each other by
performing F forward, leaving the one ring we need for eversion.
HISTORY
Sphere eversion is a relatively recent mathematical discovery.
In 1958, mathematician Stephen Smale devised an abstract formula that
proved sphere eversion was possible. It was not until the 1970s that
the (blind !) mathematician Bernard Morin came up with a visualization,
based on work by Arnold Shapiro. Morin also developed an approach in
which the sphere is represented by a polyhedron (built from flat
triangular and square faces) and then everted.
Rob Kusner with others has developed a 'minimax' eversion, which
is the 'simplest' way to evert a sphere; 'simple' in this context
meaning minimization of an 'elastic bending energy'.
REFERENCES
There is a 1966 Scientific American article on sphere eversion by Anthony Phillips,
and a computer-generated eversion by Thurston on the cover of Scientific
American, August 1993, which shows a symmetrical, 8-fold flower petal
pattern, with a balloon being blown up in the center, and the lower half
the original, shrinking sphere. However, no explanation is given in the
article itself, which is about computer proofs in mathematics. There have
been earlier articles in Scientific American which deal with everting a
torus, but only after cutting a hole in it first.
A well illustrated, *very* good introductory text on topology is:
The Shape of Space - How to Visualize Surfaces and
Three-Dimensional Manifolds. by Jeffrey R. Weeks
(1985) Marcel Dekker, Inc / New York - Basel ISBN: 0-8247-7437-X
Weeks is also the author of an article on the mathematics of
three-dimensional manifolds in Scientific American, July 1984.
The history of sphere eversion is discussed in:
Islands of Truth - a mathematical mystery cruise p. 46-
by Ivar S. Peterson (1990) W.H. Freeman & Company
Stephen Smale has received the Fields Medal (the 'Nobel prize' for
mathematics) in 1966 for his work in topology and went on to become
one of the pioneers of chaotic dynamical systems. A description of his
career can be found in:
Chaos: making a new science. by James Gleick
(1987) Viking Penguin Inc. New York ISBN: 0 14 00.9250 1
The archives of the late, great Geometry Center at the
University of Minnesota contain a good sphere eversion history:
http://www.geom.uiuc.edu/docs/outreach/oi/history.html
The brilliant 1994 video "Outside In" about sphere eversion
also originated at the Geometry Center. It includes Thurston's eversion.
https://www.youtube.com/watch?v=wO61D9x6lNY
Chris Hills has a more extensive list of eversion links at
http://www.chrishills.org.uk/ChrisHills/sphereeversion/index.html
For any questions or remarks please e-mail me at :
Erik de Neve Erik AT_usefuldreams DOT org